Exercices Corrigés Calcul Du Degré D'hyperstaticité
Exercices corrigés calcul du degré d'hyperstaticité :
Détermination du degré d’hyperstaticité :
Exercice n°01 : On propose de calculer le degré d'hyperstaticité des structures suivantes :
Nombre de réactions d'appui (r)
• structure 1 : 3 appuis encastrés ⇒ r = 3 ∗ 3 = 9
• structure 2 : 1 appui à rotule + 1 appui à rouleaux
⇒ r = 2 + 1 = 3
• structure 3 : 1 appui à rotule + 1 appui à rouleaux
⇒ r = 2 + 1 = 3
• Nombre e d'efforts annulés aux extrémités des barres et valeurs de m Comme il n'existe pour les trois
structures aucune barre pourvue à ses extrémités d'un dispositif au droit duquel l'un des efforts est nul a
priori, on peut affirmer que m = e = 0.
• Les degrés d'hyperstaticité respectifs des quatre structures sont donc les suivants :
• structure 1 : Is = (3b+r−e) − (3n−m) = (3∗6+9−0) − (3∗7−0) = 6
• structure 2 : Is = (3b+r−e) − (3n−m) = (3∗4+3−0) − (3∗4−0) = 3
• structure 3 : Is = (3b+r−e) − (3n−m) = (3∗5+3−0) − (3∗5−0) = 3
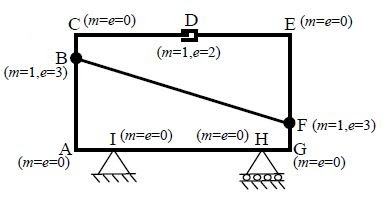
Exercice n°02 : On propose de calculer le degré d'hyperstaticité des structures suivantes :
Tout d'abord remarquons que le nombre de noeuds et de barres est le même pour les 4 structures : n = 4, b = 3.
• Nombre de réactions d'appui (r)
• structure 1 : 2 appuis encastrés ⇒ r = 2∗3 = 6
• structure 2 : 2 appuis à rotule ⇒ r = 2∗2 = 4
• structure 3 : 1 appui encastré + 1 appui à rouleaux ⇒ r = 3 + 1= 4
• structure 4 : 1 appui à rouleaux +1 appui à rotule ⇒ r = 1 + 2 = 3
• Nombre d'efforts annulés aux extrémités des barres (e)
• structure 1 : aucun dispositif de libération d'effort ⇒ e = 0
• structure 2 : 2 appuis à rotule ⇒ M annulé en A et D ⇒ e = 2
• structure 3 : 1 appui à rouleaux ⇒ M, V annulés en A ⇒ e = 2
• structure 4 : 1 appui à rouleaux +1 appui à rotule ⇒ e = 2+1 = 3
• Nombre d'équations inexploitables aux noeuds (m)
On sait que m = 1 en un noeud si l'un des trois efforts (M, N ou V) est a priori nul à
l'extrémité de chaque barre ayant ce noeud comme extrémité. Donc, si une seule barre
arrive en un noeud, alors m = e en ce noeud.
En conclusion, il y a égalité entre m et e pour les 4 structures ci-dessus .
Finalement, les degrés d'hyperstaticité respectifs des 4 structures sont les suivants :
• structure 1 : Is = (3b+r−e) − (3n−m) = (9+6−0) − (12−0) = 3
• structure 2 : Is = (3b+r−e) − (3n−m) = (9+4−2) − (12−2) = 1
• structure 3 : Is = (3b+r−e) − (3n−m) = (9+4−2) − (12−2) = 1
• structure 4 : Is = (3b+r−e) − (3n−m) = (9+3−3) − (12−3) = 0
(isostatique)
Si on introduit une rotule en C, on impose un moment nul à l'extrémité des barres BC et DC
et donc e = 2 et m = 1 en C. Le degré d'hyperstaticité des structures est donc diminué d'un
facteur (e−m) = 1. Les structures 2 et 3 deviennent isostatiques tandis que la structure 4
devient hypostatique c’est-à dire dans un état de non équilibre.
La structure des piscines du Blocry à Louvain-la-Neuve (Belgique) est un
exemple typique de structure à noeuds rigides. (Architecte Goelhen, Photo de
l'auteur).
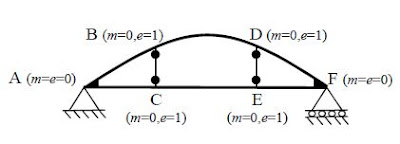
Exercice n°03 : On propose de calculer le degré d’hyperstaticité des structures suivantes :
Structure 1 : en chaque noeud B, C, D et E, e vaut 1 puisque les rotules annulent le moment fléchissant
aux extrémités des barres BC et DE. Aux noeuds A et F, e est nul puisqu'il y a continuité de la structure
en ces noeuds. En ce qui concerne le terme m, il est nul partout puisqu'il n'existe aucun noeud où un
même effort est annulé aux extrémités respectives de toutes les barres qui le joignent. Par ailleurs il
existe r=3 réactions d'appui.
Le degré d'hyperstaticité de la structure vaut donc :
(3b+r−e) − (3n−m) = (3∗8+3−4) − (3∗6−0) = 5
• Structure 2 : Le degré d'hyperstaticité de la structure vaut :
(3b+r−e) − (3n−m) = (3∗8+5−8) − (3∗8−5) = 2
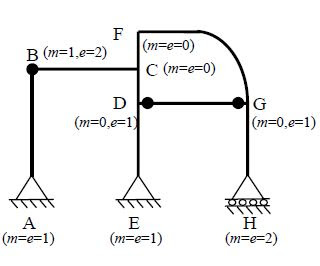
Exercice n°04 : On propose de calculer le degré d'hyperstaticité des structures suivantes :
• Structure 1 : Le degré d'hyperstaticité de la structure vaut :
(3b+r−e) − (3n−m) = (3∗10+3−8) − (3∗9−3) = 1
• Structure 2 : Le degré d'hyperstaticité de la structure vaut :
(3b+r−e) − (3n−m) = (3∗10+3−4) − (3∗9−1) = 3
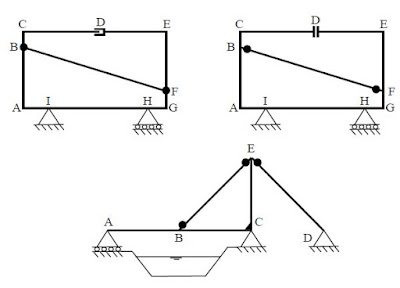
• Structure 3 : Les deux rotules situées en E annulent le moment fléchissant non seulement à
l'extrémité E des barres BE et DE (qui modélisent des câbles), mais aussi à l'extrémité de la barre CE.
Conceptuellement, on ne change donc absolument rien dans la répartition des efforts si on remplace ces
deux rotules par une rotule unique reliant les trois barres en E :
Le degré d'hyperstaticité de la structure vaut : (3b+r−e) − (3n−m) = (3∗5+5−7) − (3∗5−4) = 2
Lire Aussi : exercice avec solution béton armé b.a.e.l
dessin technique et lecture de plan principes et exercices
exemple de calcul voile de bâtiment d'habitation
mécanique des structures tom 6 exercices serge laroze
formation spéciale en robot avec exercices corrigés
calculs topométriques exercices corrigées topographie
mur de soutènement exercice calcul poussé butée td
td mecanique des sols soutènement / corrections
cours fondation des ouvrages avec des exercices
EXEMPLE CALCUL POTELET SUIVANT EUROCODE 03
td exercices et corrigé fondation profondes
bâtiment cours avec exercices corrigés
examen avec solution calcul des boulons
exemple de calcul escalier en béton armé
recueil d'exercices corriges construction métallique
calcul des poteaux suivant B.A.E.L avec des exercices
calcul poutres et plancher caquot-forfaitaire
résistance des matériaux 11 édition cours et exercices corrigés
comment calculer la pente de l'escalier
Mots clés : Tags : Keywords :








-2_Page_001-topaz-text-shapes-1x.jpg)



